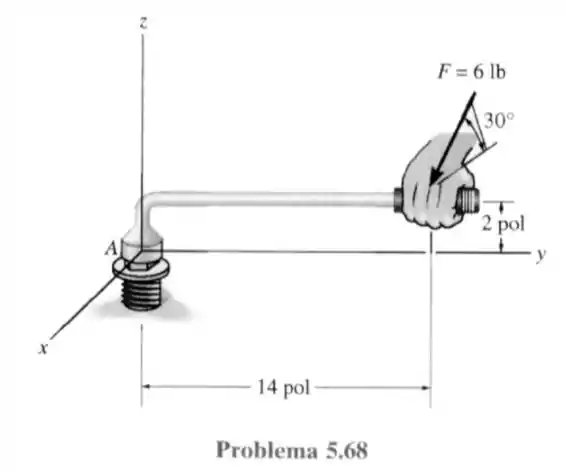
68- A chave é utilizada para apertar o parafuso em . Se a força for aplicada ao cabo da chave, como mostrado na figura, determine as intensidades da força resultante e do momento que a cabeça do parafuso exerce na chave. A força está em um plano paralelo ao plano .
Passo 1
A boca da chave resiste a força nos três sentidos em força e em torque, o que nos daria o seguinte sistema de forças.
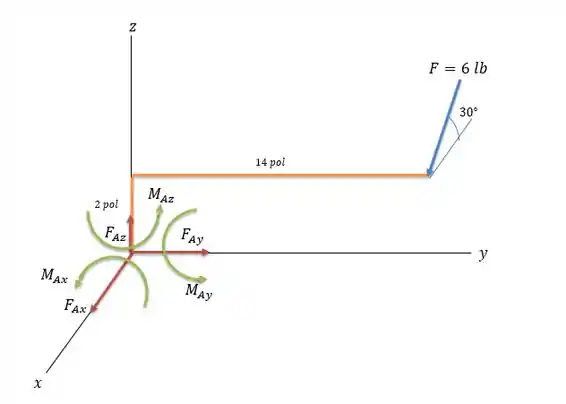
Passo 2
Se fizermos a somatória das forças em temos:
Agora fazendo a somatória das forças em :
E agora fazendo a somatória das forças :
Isso faz com que a força resultante no parafuso seja:
Passo 3
Agora para os momentos:
A força de pode ser rebatida de modo a ter força em e em a força resultante no eixo faz momento na barra de 14 pol que se encontra no eixo gerando momento em . Ou seja:
Agora a força rebatida em faz momento na barra em de 14 pol e na barra em de .
O momento gerado na barra de 14 pol gera momento em ou seja:
E a força rebatida em gera uma momento em na barra de 2 pol com direção em :
Isso faz com que o momento resultante no parafuso seja: